Grandezas Escalares – Ficam perfeitamente definidas por seus valores numéricos acompanhados das respectivas unidades de medida. Exemplos: massa, temperatura, volume, densidade, comprimento, etc.
Grandezas vetoriais – Exigem, além do valor numérico e da unidade de medida, uma direção e um sentido para que fiquem completamente determinadas. Exemplos: deslocamento, velocidade, aceleração, força, etc.
VETORES
Para representar as grandezas vetoriais, são utilizados os vetores: entes matemáticos abstratos caracterizados por um módulo, por uma direção e por um sentido.
Representação de um vetor – Graficamente, um vetor é representado por um segmento orientado de reta:
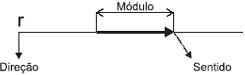
Elementos de um vetor:
Direção – Dada pela reta suporte (r) do vetor.
Módulo – Dado pelo comprimento do vetor.
Sentido – Dado pela orientação do segmento.
Resultante de vetores (vetor-soma) – Considere um automóvel deslocando-se de A para B e, em seguida, para C. O efeito desses dois deslocamentos
combinados é levar o carro de A para C. Dizemos, então, que o vetor
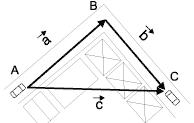
Regra do Polígono – Para determinar a resultante
Regra do paralelogramo – Os vetores são dispostos de modo que suas origens coincidam. Traçando-se um paralelogramo, que tenha
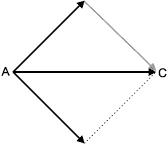
Componentes ortogonais de um vetor – A componente de um vetor, segundo uma dada direção, é a projeção ortogonal (perpendicular) do vetor naquela direção. Decompondo-se um vetor
Nenhum comentário:
Postar um comentário