Luiz Henrique Pereira da Costa
Energia (física)
A energia é um conceito de vasta aplicação em física. É uma grandeza física que tradicionalmente se definecomo a capacidade de corpos e sistemas para realizar um trabalho.
A energia pode adotar diversas formas, podendo transformar-se de uma noutra forma (conversão deenergia), embora não se crie nem se destrua (princípio da conservação da energia). Por exemplo, quandouma maçã cai, perde energia potencial gravítica, ganhando a mesma quantidade de energia cinética.
Algumas das unidades mais utilizadas são o Joule (J) (unidade do Sistema Internacional), o eletrão-volt(ev), o quilowatt-hora (kWh) e a caloria (cal).
A energia é classificada em duas formas fundamentais: energia potencial, que é a energia armazenada numcorpo ou num sistema em consequência da sua posição, forma ou estado (esta forma de energia incluienergia potencial gravítica, energia elétrica, energia nuclear e energia química) e energia cinética que é aenergia do movimento, e é usualmente definida como trabalho que será realizado sobre um corpo quepossui energia, quando ele é levado ao repouso.
O calor é outra forma de energia, que se deve à energia cinética associada aos átomos e moléculas de umasubstância.
Os primeiros a definir a noção de energia foram o físico inglês James Prescott Joule (1818-1889) e o físicofrancês Nicolas Leonard Sadi Carnot (1796-1832) em relação à conversão do calor em energia mecânica, evice-versa. Até meados do século XIX, o físico e matemático britânico William Thomson (1824-1904) e ofísico alemão Rudolf Julius Clausius (1822-1888) provaram a diminuição da capacidade de realização de umtrabalho por parte de um sistema isolado (degradação de energia). A formulação da teoria dos quanta deenergia, descoberta pelo físico alemão Max Planck (1858-1947) em 1900, para além de considerar que aenergia possui uma natureza corpuscular e descontínua, permitiu abrir o caminho para a explicação deefeitos tais como o fotoelétrico e possibilitar o nascimento da teoria quântica da radiação. Finalmente, ofísico alemão Albert Einstein (1879-1955) em 1905, ao demonstrar a equivalência entre massa e energia,constituiu a base dos processos nucleares. A teoria da relatividade de Einstein relaciona a energia E com amassa m através da equação:
E = mc2, em que c é a velocidade da luz.
Os recursos energéticos consistem no armazenamento de energia convertível. Os recursos não-renováveisincluem os combustíveis fósseis (carvão, petróleo e gás) e os combustíveis da fissão nuclear.
A 29 de maio, comemora-se o Dia Mundial da Energia.
Trabalho e Energia
Os objetos de estudo da mecânica
A energia é algo com que convivemos constantemente. Para nos mantermos vivos, precisamos nos alimentar e, para isso, extrair a energia dos alimentos. Historicamente, o homem se encontra em uma busca constante por formas de energia. A queda das águas para gerar energia elétrica, a queima de combustíveis para a geração de movimento e mais um enorme número de exemplos.
Desses todos, é importante observar que em nenhum deles ocorreu criaçãode energia, mas sim a sua transformação. Um caso clássico que pode ser citado é o de uma usina hidrelétrica, onde ocorre a transformação da energia mecânica em energia elétrica.
Aqui vamos explicar as formas de energia que são estudadas na mecânica, como o trabalho e as energias cinética, potencial e mecânica.
Note que, para realizar-se um trabalho, existe a necessidade de um deslocamento. Caso algum objeto esteja sob a ação de uma força, mas em repouso, não haverá a realização de trabalho. As forças que atuam sobre uma pessoa parada segurando uma mala não realizam
trabalho pois não há deslocamento do ponto de aplicação dessas forças.
Considere um objeto que está submetido a uma força e, devido a essa força, esse objeto sofre um deslocamento
e, devido a essa força, esse objeto sofre um deslocamento  , como se vê abaixo:
, como se vê abaixo:
A força pode ser dividida em dois componentes,
pode ser dividida em dois componentes,  e
e  , como se mostra a seguir:
, como se mostra a seguir:
Observe que o componente de que realiza o trabalho é
que realiza o trabalho é  , pois é o que tem a mesma direção do deslocamento. O componente
, pois é o que tem a mesma direção do deslocamento. O componente  não realiza trabalho, pois é perpendicular ao deslocamento e, por isso, não interfere diretamente no movimento.
não realiza trabalho, pois é perpendicular ao deslocamento e, por isso, não interfere diretamente no movimento.
O trabalho é definido como sendo o produto do componente pelo deslocamento sofrido pelo objeto e como
pelo deslocamento sofrido pelo objeto e como  , teremos a seguinte definição matemática para o trabalho:
, teremos a seguinte definição matemática para o trabalho:
No Sistema Internacional, a unidade de trabalho é o joule (J).
No exemplo citado, a força mostrada é causadora do movimento do objeto, mas existem casos em que a força é de oposição ao movimento, como por exemplo o atrito. Nessas situações o trabalho será negativo. Observe o quadro abaixo:
Uma força que merece uma atenção especial, ao realizar trabalho, é a força da gravidade. Considere um corpo que é abandonado de certa altura. Durante o movimento de queda temos um deslocamento para baixo e uma força, a gravidade, que também é direcionada para baixo. Sabemos que, se há uma força e um deslocamento do ponto de aplicação, haverá a realização de trabalho. Nesse caso o trabalho será determinado pelo produto da força da gravidade pela altura de queda do objeto:
É importante salientar que o trabalho da força da gravidade independe da trajetória descrita durante o movimento e por isso ela é classificada como força conservativa.
A força da gravidade também é conhecida como força peso que é constante quando se está próximo da superfície da Terra e é calculada com o produto da massa do objeto pela a aceleração da gravidade local.
Em uma descida, o trabalho da força da gravidade é positivo, pois ela está contribuindo com o movimento, mas, em uma subida, o trabalho da força da gravidade será negativo, pois agora ela é de oposição ao movimento.
 é o vetor que indica deslocamento.
é o vetor que indica deslocamento.
A força aplicada é determinada pela Segunda lei de Newton, ou seja:
Considerando que a força aplicada foi constante e que a bicicleta partiu do repouso, então a ela realizará um movimento uniformemente variado e o seu deslocamento e a sua velocidade serão determinadas da seguinte forma:
Substituindo as equações de força e deslocamento na definição de trabalho, teremos:
Lembre que v = a.t e então chegaremos à equação que determina o trabalho realizado pela força aplicada a essa bicicleta, para que ela atinja a velocidade v.
A expressão acima é definida como energia cinética, e expressa a capacidade de um corpo em movimento para realizar trabalho.
Observe que quanto maior for a altura inicial da pedra, tanto maior será o trabalho realizado pela força da gravidade, pois maior será o deslocamento realizado por ela. É importante perceber que a pedra entra em movimento espontâneo, ou seja, você não precisa forçar o movimento. Se isso ocorre, é porque na pedra existe uma energia armazenada que será utilizada na realização de trabalho. Essa energia é definida como energia potencial e, no caso descrito, isto é, em que a força da gravidade realiza trabalho, essa energia é definida como energia potencial gravitacional.
A energia potencial depende da posição do objeto. No caso da energia potencial gravitacional a posição é definida pela a altura em que o objeto se encontra de um nível horizontal definido como nível de referência.
Para determinar o valor da energia potencial gravitacional, basta sabermos o valor do trabalho realizado pela força peso, ou seja, a energia potencial gravitacional é numericamente igual ao trabalho da força peso.
A expressão matemática anterior é conhecida como o Teorema da Energia Cinética.
Observe também, que durante a queda, a energia potencial do corpo diminui, pois se tomarmos como nível de referência o solo, a altura do corpo em relação ao mesmo, está diminuindo. Nesse caso, o trabalho realizado pela força peso pode ser determinado pelo decréscimo da energia potencial, isto é:
As duas equações mencionadas aqui são usadas para o mesmo fim, que é a determinação do trabalho da força peso, e por isso elas são iguais. Igualando a primeira equação com a segunda, teremos:
Isolando os termos de energia cinética dos termos de energia potencial, chegamos ao seguinte resultado:
A soma da energia cinética com a energia potencial é definida como energia mecânica, e a expressão anterior mostra a sua conservação durante qualquer movimento sob ação exclusiva de forças conservativas, como por exemplo, na mecânica, a força peso e a força elástica. Sistemas físicos que se encontram sob essa situação são definidos como sistemas conservativos.
Energia mecânica 
Sistema conservativo 
No nosso dia-a-dia, é muito difícil encontrarmos um sistema conservativo. Em uma queda real existe o atrito com o ar e isso fará com que a energia mecânica inicial seja diferente da energia mecânica final, e tal diferença ocorre porque o atrito provoca a dissipação em forma de calor. Essa energia dissipada tem o seu valor, em módulo, igual à diferença da energia mecânica inicial pela energia mecânica final.
Desses todos, é importante observar que em nenhum deles ocorreu criaçãode energia, mas sim a sua transformação. Um caso clássico que pode ser citado é o de uma usina hidrelétrica, onde ocorre a transformação da energia mecânica em energia elétrica.
Aqui vamos explicar as formas de energia que são estudadas na mecânica, como o trabalho e as energias cinética, potencial e mecânica.
Trabalho
Para se colocar algum objeto em movimento, é necessária a aplicação de uma força e, simultaneamente, uma transformação de energia. Quando há a aplicação de uma força e um deslocamento do ponto de aplicação dessa força, pode-se dizer que houve uma realização de trabalho.Note que, para realizar-se um trabalho, existe a necessidade de um deslocamento. Caso algum objeto esteja sob a ação de uma força, mas em repouso, não haverá a realização de trabalho. As forças que atuam sobre uma pessoa parada segurando uma mala não realizam
trabalho pois não há deslocamento do ponto de aplicação dessas forças.
Considere um objeto que está submetido a uma força
 e, devido a essa força, esse objeto sofre um deslocamento
e, devido a essa força, esse objeto sofre um deslocamento  , como se vê abaixo:
, como se vê abaixo: |
A força
 pode ser dividida em dois componentes,
pode ser dividida em dois componentes,  e
e  , como se mostra a seguir:
, como se mostra a seguir: |
Observe que o componente de
 que realiza o trabalho é
que realiza o trabalho é  , pois é o que tem a mesma direção do deslocamento. O componente
, pois é o que tem a mesma direção do deslocamento. O componente  não realiza trabalho, pois é perpendicular ao deslocamento e, por isso, não interfere diretamente no movimento.
não realiza trabalho, pois é perpendicular ao deslocamento e, por isso, não interfere diretamente no movimento.O trabalho é definido como sendo o produto do componente
 pelo deslocamento sofrido pelo objeto e como
pelo deslocamento sofrido pelo objeto e como  , teremos a seguinte definição matemática para o trabalho:
, teremos a seguinte definição matemática para o trabalho: |
No Sistema Internacional, a unidade de trabalho é o joule (J).
No exemplo citado, a força mostrada é causadora do movimento do objeto, mas existem casos em que a força é de oposição ao movimento, como por exemplo o atrito. Nessas situações o trabalho será negativo. Observe o quadro abaixo:
 |
Uma força que merece uma atenção especial, ao realizar trabalho, é a força da gravidade. Considere um corpo que é abandonado de certa altura. Durante o movimento de queda temos um deslocamento para baixo e uma força, a gravidade, que também é direcionada para baixo. Sabemos que, se há uma força e um deslocamento do ponto de aplicação, haverá a realização de trabalho. Nesse caso o trabalho será determinado pelo produto da força da gravidade pela altura de queda do objeto:
 |
É importante salientar que o trabalho da força da gravidade independe da trajetória descrita durante o movimento e por isso ela é classificada como força conservativa.
A força da gravidade também é conhecida como força peso que é constante quando se está próximo da superfície da Terra e é calculada com o produto da massa do objeto pela a aceleração da gravidade local.
 |
Em uma descida, o trabalho da força da gravidade é positivo, pois ela está contribuindo com o movimento, mas, em uma subida, o trabalho da força da gravidade será negativo, pois agora ela é de oposição ao movimento.
 |
 é o vetor que indica deslocamento.
é o vetor que indica deslocamento.Energia Cinética
Considere um corpo inicialmente em repouso, como por exemplo, uma bicicleta. Para colocá-la em movimento será necessária a aplicação de uma força e, com isso, a realização de trabalho. Se essa força for paralela ao deslocamento, o trabalho será determinado pelo produto da força pelo deslocamento. |
A força aplicada é determinada pela Segunda lei de Newton, ou seja:
 |
Considerando que a força aplicada foi constante e que a bicicleta partiu do repouso, então a ela realizará um movimento uniformemente variado e o seu deslocamento e a sua velocidade serão determinadas da seguinte forma:
 |
Substituindo as equações de força e deslocamento na definição de trabalho, teremos:
 |
Lembre que v = a.t e então chegaremos à equação que determina o trabalho realizado pela força aplicada a essa bicicleta, para que ela atinja a velocidade v.
 |
A expressão acima é definida como energia cinética, e expressa a capacidade de um corpo em movimento para realizar trabalho.
 |
Energia potencial gravitacional
Estamos todos submetidos a uma força da gravidade e essa força é praticamente constante quando se está próximo à superfície do planeta. Agora, imagine-se segurando uma pedra a certa altura do solo. Para fazê-la entrar em movimento, basta largá-la e durante a queda haverá a realização de trabalho pela força gravitacional.Observe que quanto maior for a altura inicial da pedra, tanto maior será o trabalho realizado pela força da gravidade, pois maior será o deslocamento realizado por ela. É importante perceber que a pedra entra em movimento espontâneo, ou seja, você não precisa forçar o movimento. Se isso ocorre, é porque na pedra existe uma energia armazenada que será utilizada na realização de trabalho. Essa energia é definida como energia potencial e, no caso descrito, isto é, em que a força da gravidade realiza trabalho, essa energia é definida como energia potencial gravitacional.
A energia potencial depende da posição do objeto. No caso da energia potencial gravitacional a posição é definida pela a altura em que o objeto se encontra de um nível horizontal definido como nível de referência.
 |
Para determinar o valor da energia potencial gravitacional, basta sabermos o valor do trabalho realizado pela força peso, ou seja, a energia potencial gravitacional é numericamente igual ao trabalho da força peso.
 |
Energia mecânica
Considere novamente um corpo em queda. Durante esse movimento, observamos que, ao longo do trabalho realizado pela força peso, ocorre um aumento da energia cinética, pois há um aumento de velocidade. O trabalho da força peso realizado durante esse movimento pode ser determinado pela variação da energia cinética, ou seja: |
A expressão matemática anterior é conhecida como o Teorema da Energia Cinética.
Observe também, que durante a queda, a energia potencial do corpo diminui, pois se tomarmos como nível de referência o solo, a altura do corpo em relação ao mesmo, está diminuindo. Nesse caso, o trabalho realizado pela força peso pode ser determinado pelo decréscimo da energia potencial, isto é:
 |
As duas equações mencionadas aqui são usadas para o mesmo fim, que é a determinação do trabalho da força peso, e por isso elas são iguais. Igualando a primeira equação com a segunda, teremos:
 |
Isolando os termos de energia cinética dos termos de energia potencial, chegamos ao seguinte resultado:
 |
A soma da energia cinética com a energia potencial é definida como energia mecânica, e a expressão anterior mostra a sua conservação durante qualquer movimento sob ação exclusiva de forças conservativas, como por exemplo, na mecânica, a força peso e a força elástica. Sistemas físicos que se encontram sob essa situação são definidos como sistemas conservativos.


No nosso dia-a-dia, é muito difícil encontrarmos um sistema conservativo. Em uma queda real existe o atrito com o ar e isso fará com que a energia mecânica inicial seja diferente da energia mecânica final, e tal diferença ocorre porque o atrito provoca a dissipação em forma de calor. Essa energia dissipada tem o seu valor, em módulo, igual à diferença da energia mecânica inicial pela energia mecânica final.
 |
Não existe uma definição do que é energia, mas sabemos que a sua existência possibilita a execução de trabalho. A energia armazenada nos alimentos, por exemplo, faz com que os órgãos do corpo de uma pessoa funcionem corretamente. Os combustíveis fazem com que os veículos automotores se locomovam. Da mesma forma, a energia elétrica produzida pela bateria faz com que os elétrons dos fios condutores de energia se locomovam.
Ao falar de energia é de extrema importância ressaltar o Princípio de Conservação da Energia. Princípio este que, segundo Lavoisier, diz: “Na natureza nada se perde, nada se cria, tudo se transforma”.
De forma a exemplificar conversões de energia de um modo geral, consideremos uma mola relaxada (figura 1), ou seja, uma mola que não está esticada. Veja:
Ao falar de energia é de extrema importância ressaltar o Princípio de Conservação da Energia. Princípio este que, segundo Lavoisier, diz: “Na natureza nada se perde, nada se cria, tudo se transforma”.
De forma a exemplificar conversões de energia de um modo geral, consideremos uma mola relaxada (figura 1), ou seja, uma mola que não está esticada. Veja:
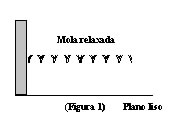
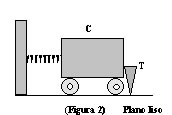
Para comprimir a mola é necessário um gasto de energia. Assim, aplica-se uma força em uma de suas extremidades, de forma que a mesma se contraia. Dizemos que ao se aplicar a força sobre a mola há a realização de um trabalho. Este trabalho corresponde à energia transferida da pessoa para a mola. A figura 2 representa a mola já comprimida e com uma trava no carrinho, impedindo que o mesmo se liberte.
A mola comprimida armazena energia. Essa energia, porém, só pode ser manifestada ao se retirar a trava do carrinho. A energia armazenada na mola é denominada de Energia Potencial Elástica. Potencial porque pode se manifestar e elástica porque está em um corpo elástico deformado.
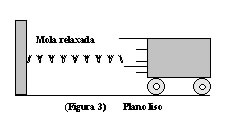
Agora, observando a figura 3, percebemos que o carrinho se libertou. Ao ser retirada a trava, a energia potencial que estava armazenada na mola se manifestou, fazendo com que o carrinho adquirisse movimento. Novamente temos a realização de trabalho. Agora esse trabalho corresponde à energia transferida da mola para o carrinho. A energia que o carrinho adquiriu é denominada de Energia Cinética.
Energia Cinética: é a energia que está relacionada ao movimento dos corpos.
Energia Potencial (gravitacional, elástica, elétrica, etc.): é a energia que um corpo possui em relação à posição particular que ele ocupa.
Na ausência de atrito, a energia mecânica total de um sistema se conserva, havendo apenas a transformação de energia potencial em energia cinética e vice-versa. Veja:
Emec= Ec + Ep
É de grande importância deixar bem claro que o trabalho e as formas de energia são grandezas escalares.
Trabalho de uma força
Trabalho é a medida da energia que é transferida para um corpo, em razão da aplicação de uma força ao longo de um deslocamento. Em Física, trabalho é normalmente representado por W(que vem do inglês work) ou mais usadamente a letra grega tau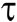 .
.
Para calcular o trabalho de uma força é importante ressaltar que ele pode ser:
Trabalho de uma força constante e paralela ao deslocamento: é calculado quando se tem a força sendo aplicada no mesmo sentido do deslocamento. Pode ser calculado da seguinte forma:
A mola comprimida armazena energia. Essa energia, porém, só pode ser manifestada ao se retirar a trava do carrinho. A energia armazenada na mola é denominada de Energia Potencial Elástica. Potencial porque pode se manifestar e elástica porque está em um corpo elástico deformado.
Agora, observando a figura 3, percebemos que o carrinho se libertou. Ao ser retirada a trava, a energia potencial que estava armazenada na mola se manifestou, fazendo com que o carrinho adquirisse movimento. Novamente temos a realização de trabalho. Agora esse trabalho corresponde à energia transferida da mola para o carrinho. A energia que o carrinho adquiriu é denominada de Energia Cinética.
Energia Cinética: é a energia que está relacionada ao movimento dos corpos.
Energia Potencial (gravitacional, elástica, elétrica, etc.): é a energia que um corpo possui em relação à posição particular que ele ocupa.
Na ausência de atrito, a energia mecânica total de um sistema se conserva, havendo apenas a transformação de energia potencial em energia cinética e vice-versa. Veja:
Emec= Ec + Ep
É de grande importância deixar bem claro que o trabalho e as formas de energia são grandezas escalares.
Trabalho de uma força
Trabalho é a medida da energia que é transferida para um corpo, em razão da aplicação de uma força ao longo de um deslocamento. Em Física, trabalho é normalmente representado por W(que vem do inglês work) ou mais usadamente a letra grega tau
Para calcular o trabalho de uma força é importante ressaltar que ele pode ser:
Trabalho de uma força constante e paralela ao deslocamento: é calculado quando se tem a força sendo aplicada no mesmo sentido do deslocamento. Pode ser calculado da seguinte forma:
Como o ângulo entre a força e o deslocamente é zero faz com que o cosseno deste ângulo seja igual a 1, tornando a expressão equivalente à:
Onde D é o deslocamento sofrido pelo corpo.
Trabalho de uma força constante e não paralela ao deslocamento:
Trabalho de uma força constante e não paralela ao deslocamento:
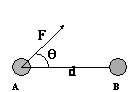
Quando temos a aplicação da força constante e não paralela, como no esquema acima, calculamos o trabalho da seguinte forma:
Onde ? é o ângulo formado entre a força e o deslocamento sofrido pelo corpo.
No SI (Sistema Internacional de Unidades) o trabalho é dado em joule, que é representado pela letra (J) e a força é dada em newton (N). Essa unidade é uma homenagem ao físico britânico James Prescott Joule. No sistema CGS, a unidade de trabalho é o erg= dina x centímetro.
- Energias Potencial e Cinética
Todo o corpo, ainda que se encontre em repouso, tem "guardada", ou mais propriamente armazenada energia, que se designada por "energia potencial", e que se representa por "Ep".
Existem três tipo de energia potencial, cuja definição não está considerada no âmbito deste artigo, e que são os seguintes:
- Gravitacional.
- Elástica.
- Química.
A energia cinética, que, como vimos, representa o trabalho realizado por uma força aplicada a um corpo, e que portanto resulta da transformação da sua energia potencial, é calculada de acordo com a seguinte fórmula:
“Ec = (m * v2) / 2”
A grandeza “m” representa a massa do corpo e “v” a velocidade de que o corpo fica animado pela aplicação da força.
A velocidade do corpo calcula-se de acordo com a seguinte fórmula:
“v = e/t”, onde "e" representa o espaço e "t" o tempo.
Assim a equação da energia cinética pode escrever-se da seguinte forma:
"Ec = (m*e2) / (2*t2)"
Na figura 2 apresenta-se um exemplo onde estão representadas a "energia potencial" e a "energia cinética". - 2Teorema da Energia Cinética
O “teorema da energia cinética” permite calcular o trabalho realizado pela totalidade das forças que actuam nesse sistema, e é enunciado da seguinte forma:
“ A totalidade do trabalho produzido por todas as forças que atuam num determinado sistema é calculado pela variação da energia cinética do sistema”. - 3Lei da Conservação da Energia
A “lei da conservação da energia” diz que:
“Num sistema isolado, isto é, sem sofrer a influência de qualquer fator externo, a quantidade total de energia permanece constante”.
Esta lei pode apresentar-se da seguinte forma:
“E = Ep + Ec”, onde “E” representa a “energia total.
Esta lei traduz a célebre afirmação de Lavoisier.
"Na natureza nada se cria, nada se perde, tudo se transforma".
De acordo com a “Teoria da Relatividade” de Einstein, a energia de um corpo é calculada pela fómula:
“E = m * c2”, onde “m” representa a massa do corpo e “c” a velocidade da luz (300.000 km/s). - 4Sistema de Unidades
No Sistema Internacional de Unidades (que se representa por SI) as unidades que iremos utilizar neste artigo são as seguintes:
- “Energia” (símbolo “E”): “joule” (símbolo “J”).
- "Massa" (símbolo "m"): "quilograma (símbolo: "kg").
- “Comprimento/Espaço” (símbolo “l/e”): “metro” (símbolo “m”).
- “Tempo” (símbolo “t”): “segundo” (símbolo “s”).Exercício resolvido: Energia Potencial, Energia Elástica
Exercício de Física do vestibular da FATEC-SP 2002. Prova de número 2, questão que exige conhecimentos de mecânica: conservação de energia, energia potencial, energia elástica.
(FATEC 2002) Um bloco de massa 0,60kg é abandonado, a partir do repouso, no ponto A de uma pista no plano vertical. O ponto A está a 2,0m de altura da base da pista, onde está fixa uma mola de constante elástica 150 N/m. São desprezíveis os efeitos do atrito e adota-se g=10m/s2. A máxima compressão da mola vale, em metros:
A máxima compressão da mola vale, em metros:
a) 0,80
b) 0,40
c) 0,20
d) 0,10
e) 0,05Resolução
Sabendo que o sistema não tem perda de energia e, pela lei de conservação de energia temos:
Energia inicial = Energia final
Energia potencial ( mgh ) = Energia elástica ( kx2/2 )
mgh=kx2/2
0,60 . 10 . 2,0 = (150 . x2) / 2
24 = 150 . x2
x2 = 24 / 150
x2 = 0,16
x = 0,4 m
Obtemos então, como resposta a alternativa B.A SEGUIR LINK DE UM DOS MELHOR EXERCÍCIOS DE ENERGIA JÁ BEM TRABALHADOS QUE JÁ VI:http://wwwp.fc.unesp.br/~malvezzi/downloads/Ensino/Disciplinas/FisicaI_Eng/ListaCap07.pdf
Espero que tenha ajudado vocês. Bjos
Nenhum comentário:
Postar um comentário