FORÇA DE ATRITO, FORÇA ELÁSTICA, FORÇA CENTRÍPETA E PLANO INCLINADO.

Força de Atrito

Até agora, para calcularmos a força, ou aceleração de um corpo, consideramos que as superfícies por onde este se deslocava, não exercia nenhuma força contra o movimento, ou seja, quando aplicada uma força, este se deslocaria sem parar.

Mas sabemos que este é um caso idealizado. Por mais lisa que uma superfície seja, ela nunca será totalmente livre de atrito.

Sempre que aplicarmos uma força a um corpo, sobre uma superfície, este acabará parando.

É isto que caracteriza a força de atrito:

Se opõe ao movimento;
Depende da natureza e da rugosidade da superfície (coeficiente de atrito);
É proporcional à força normal de cada corpo;
Transforma a energia cinética do corpo em outro tipo de energia que é liberada ao meio.

A força de atrito é calculada pela seguinte relação:

Onde:

μ: coeficiente de atrito (adimensional)

N: Força normal (N)

Atrito Estático e Dinâmico

Quando empurramos um carro, é fácil observar que até o carro entrar em movimento é necessário que se aplique uma força maior do que a força necessária quando o carro já está se movimentando.

Isto acontece pois existem dois tipo de atrito: o estático e o dinâmico.

Atrito Estático

É aquele que atua quando não há deslizamento dos corpos.

A força de atrito estático máxima é igual a força mínima necessária para iniciar o movimento de um corpo.

Quando um corpo não está em movimento a força da atrito deve ser maior que a força aplicada, neste caso, é usado no cálculo um coeficiente de atrito estático: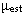

Então:

Atrito Dinâmico

É aquele que atua quando há deslizamento dos corpos.

Quando a força de atrito estático for ultrapassada pela força aplicada ao corpo, este entrará em movimento, e passaremos a considerar sua força de atrito dinâmico.

A força de atrito dinâmico é sempre menor que a força aplicada, no seu cálculo é utilizado o coeficiente de atrito cinético: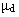

Então:

Força Elástica

Imagine uma mola presa em uma das extremidades a um suporte, e em estado de repouso (sem ação de nenhuma força).

Quando aplicamos uma força F na outra extremidade, a mola tende a deformar (esticar ou comprimir, dependendo do sentido da força aplicada).

Ao estudar as deformações de molas e as forças aplicadas, Robert Hooke (1635-1703), verificou que a deformação da mola aumenta proporcionalmente à força. Daí estabeleceu-se a seguinte lei, chamada Lei de Hooke:

Onde:

F: intensidade da força aplicada (N);

k: constante elástica da mola (N/m);

x: deformação da mola (m).

A constante elástica da mola depende principalmente da natureza do material de fabricação da mola e de suas dimensões. Sua unidade mais usual é o N/m (newton por metro) mas também encontramos N/cm; kgf/m, etc.

Exemplo:

Um corpo de 10kg, em equilíbrio, está preso à extremidade de uma mola, cuja constante elástica é 150N/m. Considerando g=10m/s², qual será a deformação da mola?

Se o corpo está em equilíbrio, a soma das forças aplicadas a ela será nula, ou seja:

, pois as forças tem sentidos opostos.

Força Centrípeta

Quando um corpo efetua um Movimento Circular, este sofre uma aceleração que é responsável pela mudança da direção do movimento, a qual chamamos aceleração centrípeta, assim como visto no MCU.

Sabendo que existe uma aceleração e sendo dada a massa do corpo, podemos, pela 2ª Lei de Newton, calcular uma força que assim como a aceleração centrípeta, aponta para o centro da trajetória circular.

A esta força damos o nome: Força Centrípeta. Sem ela, um corpo não poderia executar um movimento circular.

Como visto anteriormente, quando o movimento for circular uniforme, a aceleração centrípeta é constante, logo, a força centrípeta também é constante.

Sabendo que:

Então:

A força centrípeta é a resultante das forças que agem sobre o corpo, com direção perpendicular à trajetória.

Exemplo:

Um carro percorre uma curva de raio 100m, com velocidade 20m/s. Sendo a massa do carro 800kg, qual é a intensidade da força centrípeta?

Plano Inclinado

Dadas duas trajetórias:

Em qual delas é "mais fácil" carregar o bloco?

Obviamente, na trajetória inclinada, pois no primeiro caso, teremos que realizar uma força que seja maior que o peso do corpo. Já no segundo caso, Defermos fazer uma força que seja maior que uma das componentes de seu peso, neste caso, a componete horizontal, que terá instensidade menor conforme o ângulo formado for menor.

Por isso, no nosso cotidiano, usamos muito o plano inclinado para facilitar certas tarefas.

Ao analizarmos as forças que atuam sobre um corpo em um plano inclinado, temos:

A força Peso e a força Normal, neste caso, não tem o mesma direção pois, como já vimos, a força Peso, é causada pela aceleração da gravidade, que tem origem no centro da Terra, logo a força Peso têm sempre direção vertical. Já a força Normal é a força de reação, e têm origem na superfície onde o movimento ocorre, logo tem um ângulo igual ao plano do movimento.

Para que seja possível realizar este cálculo devemos estabelecer algumas relações:

Podemos definir o plano cartesiano com inclinação igual ao plano inclinado, ou seja, com o eixo x formando um ângulo igual ao do plano, e o eixo y, perpendicular ao eixo x;
A força Normal será igual à decomposição da força Peso no eixo y;
A decomposição da força Peso no eixo x será a responsável pelo deslocamento do bloco;
O ângulo formado entre a força Peso e a sua decomposição no eixo y, será igual ao ângulo formado entre o plano e a horizontal;
Se houver força de atrito, esta se oporá ao movimento, neste caso, apontará para cima.

Sabendo isto podemos dividir as resultantes da força em cada direção:
Em y:

como o bloco não se desloca para baixo e nem para cima, esta resultante é nula, então:

mas

então:

Em x:

mas

então:

Exemplo:

Um corpo de massa 12kg é abandonado sobre um plano inclinado formando 30° com a horizontal. O coeficiente de atrito dinâmico entre o bloco e o plano é 0,2. Qual é a aceleração do bloco?